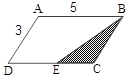شرکت در آزمون آنلاین هندسه 1 - فصل سوم: چند ضلعی ها

1

مساحت ذوزنقۀ ABCD برابر کدام است؟

۱۶

۱۸

۲۰

۲۲

2

در متوازی‌الاضلاع $ABCD$، M و N به ترتیب وسط‌های اضلاع AD و BC هستند. قطر AC را رسم می‌کنیم تا پاره‌خط‌های MB و DN را به ترتیب در P و Q قطع کند. اگر $AB = a$ و $AD = b$ و $A\hat BC = 60^\circ $ باشد، طول پاره‌خط PQ برحسب a و b کدام است؟

$\frac{۱}{۳}\sqrt {{a^۲} + {b^۲} + ab} $

$\frac{۲}{۳}\sqrt {{a^۲} + {b^۲} + ab} $

$\frac{۱}{۳}\sqrt {{a^۲} + {b^۲} - ab} $

$\frac{۲}{۳}\sqrt {{a^۲} + {b^۲} - ab} $

3

در لوزی$ABCD$، نیمساز زاویه$A$ را رسم می‌کنیم و روی آن پاره‌خط$AK$ برابر با$KD$ جدا می‌کنیم. اگر بدانیم $O$ محل برخورد دو قطر لوزی است و$\frac{{AK}}{{KO}} = 2$، اندازۀ زاویه$A$ چقدر است؟

${۳۰^ \circ }$

${۴۵^ \circ }$

${۶۰^ \circ }$

${۷۵^ \circ }$

4

در شکل مقابل نیمساز زاویۀ $\hat B$، ضلع DC را در $E$ قطع کرده است؛ مساحت ناحیۀ هاشورخورده چند برابر مساحت ذوزنقۀ ABED است؟

$\frac{۲}{۳}$

$\frac{۲}{۵}$

$\frac{۳}{۷}$

$\frac{۴}{۷}$

5

در مثلث C‏B‏A‏ ، اگر طول اضلاع B‏A‏ ، C‏A‏ و C‏B‏ به ترتیب برابر با ۶‏ و ۴‏ و ۳‏ باشد، آن‌گاه حاصل

\frac{h_{b}}{h_{c}} + \frac{h_{a}}{h_{b}} + \frac{h_{c}}{h_{a}}

چه‌قدر است؟

\frac{۳}{١۰}

\frac{١۰}{۳}

\frac{۵}{۳}

\frac{۳}{۵}

شرکت در آزمون آنلاین هندسه 1 - فصل سوم: چند ضلعی ها | آزمون شماره 4157

جست و جو

شرکت در آزمون آنلاین هندسه 1 - فصل سوم: چند ضلعی ها | آزمون شماره 4157

جست و جو

ساخت آزمون

ساخت آزمون