شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل ششم : حد و پیوستگی

1- تابع $f(x) = \left\{ \begin{array}{l}a{x^2} + {2^{x - 2}}\,\,\,\,\,\,\,\,\,\,x \ge 2\\x + a{\log _4}x\,\,\,\,\,\,\,\,x < 2\end{array} \right.$ در $x = 2$ پیوسته است. $f(7)$ کدم است؟

۳۵

۳۹

۴۳

۴۶

2-

تابع $f(x)=[\frac{x}{۳}]$ روی بازه (k,۶ ) پیوسته است . کمترین مقدار k کدام است ؟

۵

۳

$\frac{۵}{۳}$

$\frac{۴}{۳}$

3- اگر $f(x) = \mathop {\lim }\limits_{a \to 0} \frac{{{{(x + a)}^3} - {{(x + 2a)}^3}}}{a}$ باشد، حاصل $f(\sqrt 5 ) + f(\sqrt 7 )$ چقدر است؟

$ - ۱۵$

${(\sqrt ۵ + \sqrt ۷ )^۳}$

$۳(\sqrt ۵ + \sqrt ۷ )$

$ - ۳۶$

4- در تابع با ضابطۀ \[f(x) = \left\{ \begin{array}{l}\sqrt {1 - x} \,\,\,\,\,\,\,x > 0\\ - \sqrt {1 + x} \,\,\,\,x \le 0\end{array} \right.\]، حاصل \[\mathop {\lim }\limits_{x \to {0^ - }} f({x^3} - x)\] کدام است؟

\[ - ۱\]

۱

صفر

\[ - ۲\]

5-

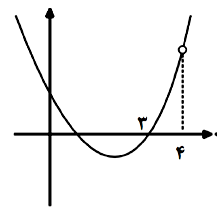
نمودار تابع $y=\frac{(x-۲)(x-a)(x-b)}{x-۴}$ به صورت زیر است. $a+b$ کدام است؟