شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 4000
1- در مثلث قائم‌الزاویۀ \[(\hat A = 90^\circ )\mathop {ABC}\limits^\Delta \] تفاضل و مجموع طول اضلاع قائم به ترتیب 1 و 7 می‌باشد. اگر میانه و ارتفاع وارد بر وتر، وتر را به ترتیب در نقاط M و H قطع کنند، $MH \times BC$ کدام است؟
2-
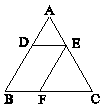
در شكل زير، اگر $\frac{{AD}}{{AB}} = \frac{2}{5}$ باشد، مساحت متواز‌ي‌الاضلاع DEFB چند برابر مثلث است؟
3-
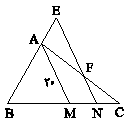
در مثلث با طول ميانۀ $AM = 20$، نقطۀ N بر روی BC را چنان انتخاب می‌کنیم که $\frac{{CN}}{{BN}} = \frac{3}{4}$ و از نقطۀ N خطی موازی AM می‌کشیم تا AC را در F و امتداد AB را در E قطع کند. طول پاره‌خط EF کدام است؟
4- در شکل زیر \[\hat A = 90^\circ \] می‌باشد. با توجه به اندازه‌های داده شده اندازة بزرگ‌ترین ارتفاع مثلث کدام است؟
5- در مثلث قائم الزاویه \[A\mathop B\limits^\Delta C\]از وسط ضلع AC عمودی بر وتر BC رسم نموده‌ایم و 4=HC و 9=BC طول ضلع AB چقدر است؟