شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل پنجم : توابع نمایی و لگاریتمی
| آزمون شماره 66
نمودار تابع \[f(x) = {4^{\,ax + b}}\]، نمودار تابع \[y = {x^2} + x - 4\] را در دو نقطه به طولهای 2 و 4 قطع میکند. حاصل \[{\log _{4a}}(8 - b)\] کدام است؟
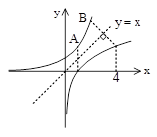
شکل مقابل، نمودار تابع $y = {2^x}$ و وارونش را نشان میدهد. طول پارهخط AB کدام است؟
اگر ${\log _a}b = \frac{1}{2}$ و ${\log _a}c = 3$ باشند، حاصل ${\log _b}(\frac{{{b^2}}}{{c\sqrt a }})$ کدام است؟
خط $\text{y}=-۱$ در کدام طول، نمودار تابع $\text{f}\left( \text{x} \right)=\text{log}_{۳}^{\frac{\text{x}+۱}{۲}}+۱$ را قطع میکند؟
اگر $\text{f}\left( \text{x} \right)={{۲}^{-\text{x}}}$ باشد، کدام تابع از ناحیه اول عبور نمیکند؟
