شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 129
ذوزنقه با طول قاعدههای 4 و 9 و ساقهای به طول 5 و 7 مفروضاند. محیط مثلث بزرگتری که از برخورد امتدادهای دو ساق ذوزنقه به دست میآید. کدام است؟
در شکل مقابل اگر $AD = 2$، $DF = 3$ و $EF = 4$ باشد، طول BC کدام است؟
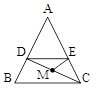
در شکل روبهرو \[DE||BC\] و M وسط DC است. اگر \[{S_{\mathop {DEM}\limits^\Delta }} = \frac{1}{4}{S_{\mathop {ADE}\limits^\Delta }}\] آنگاه مساحت ذوزنقة DECB چند برابر مساحت مثلث ADE است؟
اگر $\frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = \frac{a}{b}$، حاصل عبارت ${(\frac{{a - c}}{{b - c}})^2}$ با کدام گزینه برابر است؟ (همۀ مخرجها مخالف صفر است.)
در شکل روبهرو ABCD مستطیل و MBCN مربع است. اگر $AD = 1$ و $AB = 4$ باشد، نسبت $\frac{{PB}}{{DP}}$ کدام است؟
