شرکت در آزمون آنلاین هندسه 2 - فصل دوم : تبدیل های هندسی | آزمون شماره 26

نقطۀ M روی محیط دایرۀ \[C(O,3)\] قرار دارد. مجانس این دایره نسبت به نقطۀ M و با نسبت تجانس 3، دایرۀ \[C'(O',R')\] است. طول خط‌المرکزین دو دایره کدام است؟

تصویر دایره$C$ با شعاع 1 واحد، تحت تجانس به مرکز مبدأ و با نسبت 3، دایره$C'$ است، به‌طوری‌که خط‌المرکزین این دو دایره$2\sqrt 5 $ می‌باشد. طول مماس مشترک خارجی این دو دایره کدام است؟

فرض کنید $M'$ مجانس نقطة M به مرکز O و نسبت $\frac{1}{4}$ باشد اگر $MM' = 12$ باشد، حاصل $O{M^2} + O{M'^2}$ کدام است؟

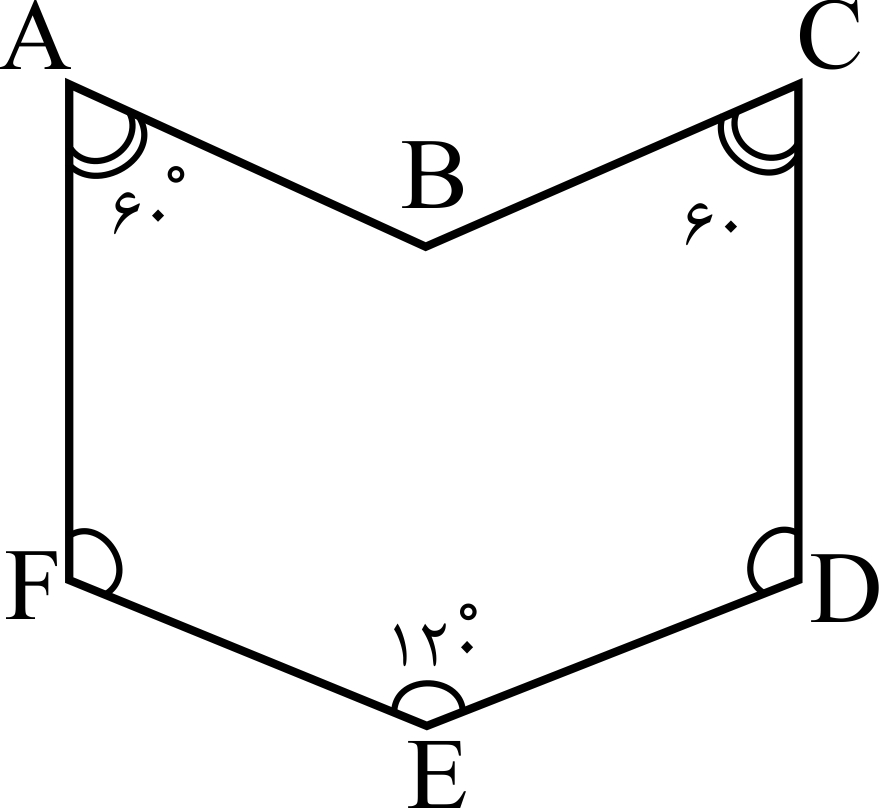
شکل مقابل، شش ضلعی ای را نشان می دهد که در آن همه اضلاع با هم برابرند $\hat{D}=\hat{E}=\hat{F}=۱۲۰^{\circ}, \hat{A}=\hat{C}=۶۰^{\circ}$ اگر بخواهیم با جابجا کردن رئوس، این شش ضلعی را به شکل بسته دیگری با همین اضلاع تبدیل کنیم، مساحت شکل حداکثر چند درصد افزایش می یابد؟

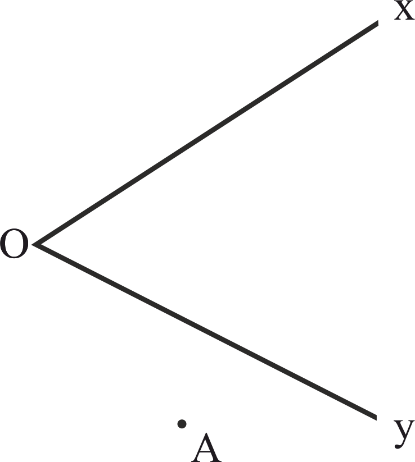
 با توجه به شکل مقابل $\widehat{xOy}=۶۰{}^\circ $ و $OA=۲$ واحد می‌باشد. بازتاب نقطه $A$ نسبت به محور $oy$ را $A'$ و بازتاب $A'$ نسبت به محور $Ox$ را $A''$ می‌نامیم. مساحت مثلث $AOA''$ کدام است؟