شرکت در آزمون آنلاین
هندسه 1
-
فصل سوم: چند ضلعی ها
| آزمون شماره 609
در متوازی‌الاضلاع ABCD، M و N به ترتیب وسط اضلاع DC و BC می‌باشند. مساحت مثلث BEM چه کسری از مساحت مثلث $\mathop {AEF}\limits^\Delta $ است؟
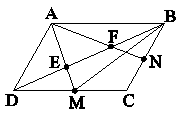
کدام گزینه صحیح است؟
در ذوزنقة مقابل \[MN||AB\] و \[\frac{{AM}}{{MD}} = 3\] است. در این صورت اندازة PQ کدام است؟
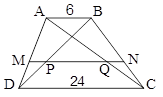
متوازی‌الاضلاع ABCD را در نظر بگیرید. نقطه P درون مثلث ABD را طوری انتخاب کرده‌ایم که مساحت مثلث ADP برابر 2 و مساحت مثلث PDC برابر 5 واحد باشد. مساحت مثلث PDB کدام است؟
مجموع فواصل هر نقطه از درون مثلث متساوی‌الاضلاعی از سه ضلع آن برابر \[4\sqrt 3 \] می‌باشد. مساحت این مثلث چقدر است؟