شرکت در آزمون آنلاین ریاضی هشتم - توازی و تعامد

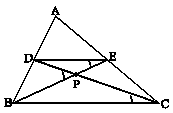
داخل مثلث $\mathop {ABC}\limits^\Delta $ خط DE را موازی ضلع BC رسم می‌کنیم. از D به C و از E به B وصل می‌کنیم تا یکدیگر را در P قطع کنند. اگر ${E_1} = 20^\circ $ و ${\hat C_1} = {10^ \circ }$ باشند، اندازة زاویه ${\hat P_1}$ کدام است؟

$۱۵^\circ $

$۲۵^\circ $

$۵۰^\circ $

$۳۰^\circ $

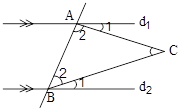
در شکل مقابل AC نیمساز زاویه ی \[\mathop {xAB}\limits^ \wedge \] می باشد و \[\mathop {2CBz}\limits^ \wedge = \mathop {CBy}\limits^ \wedge \] اگر \[{d_1}{\left\| d \right._2}\] باشد اندازه ی زاویه ی \[\mathop C\limits^ \wedge \] کدام است ؟

\[25\]

\[35\]

\[45\]

\[55\]

در شکل مقابل اگر خطوط \[{d_1}\] و \[{d_2}\] موازی باشند و \[{\hat A_2} = 2{\hat A_1}\] و \[{\hat B_2} = 2{\hat B_1}\]، در این صورت اندازه‌ی زاویه‌ی \[\hat C\] کدام است؟