شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل ششم : حد و پیوستگی

1-

اگر $f(x)=\begin{cases}a&x>۱\\-a&x<۱\end{cases}$ و $g(x)=\begin{cases}-a&x>۱\\a&x<۱\end{cases}$ باشد، آنگاه کدام تابع در x=۱ حد ندارد؟ ( $a≠۰$ )

$f(x)+ g(x)$

$f(x)- g(x)$

$f(x)\times g(x)$

$\frac{f(x)}{g(x)}$

2-

به ازای چه مقدار k تابع با ضابطه $f(x)=\left\{\begin{matrix}k+\sin(\frac{\pi x}{۲})\, \, &x>۱ & \\ \cos(\frac{\pi x}{۳})-kx\, \, &x<۱ & \end{matrix}\right.$ در نقطه $x_{۰}=۱$ دارای حد است؟

$\frac{۱}{۴}$

$\frac{۱}{۲}$

$\frac{-۱}{۲}$

$\frac{-۱}{۴}$

3-

در شکل زیر نمودار تابع $f$ داده شده است. حد تابع $y=\left\{ \begin{matrix} ۱-f\left( x \right)~~~~~~~x<۲ \\ f\left( x \right)+۱~~~~~~~۲<x\le۴ \\\end{matrix} \right.$ در چند نقطه برابر صفر است؟

۱

۲

۳

۴

4-

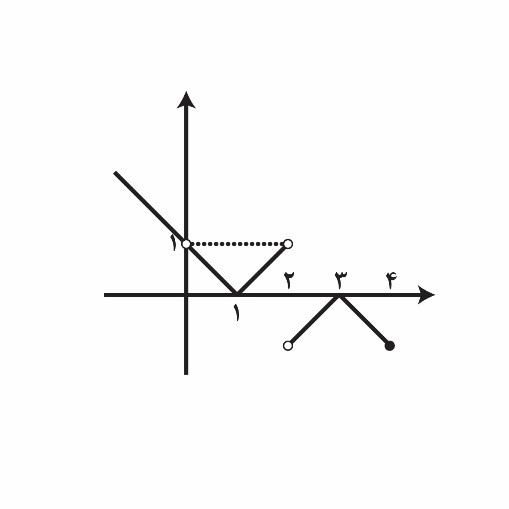
اگر $\underset{x\to \frac{۱}{۲}}{\mathop{\lim }}\,\frac{mx-\left[ x \right]}{۲-x}=۳$ آنگاه $\text{m}$ کدام است؟

$۱$

$۹$

$۶$

$۴$

5-

کدامیک از توابع زیر در $\text{x}=۰$ پیوسته است؟

$\text{y}=\left[ -\sin \text{x} \right]$

$\text{y}=\left[ -\cos \text{x} \right]$

$\text{y}=\left[ -{{\text{x}}^{۲}} \right]$

$\text{y}=\left[ {{\text{x}}^{۲}}-\text{x} \right]$

شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل ششم : حد و پیوستگی | آزمون شماره 350

جست و جو

شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل ششم : حد و پیوستگی | آزمون شماره 350

جست و جو

ساخت آزمون

ساخت آزمون