شرکت در آزمون آنلاین
حسابان 1
-
فصل پنجم : حد و پیوستگی
| آزمون شماره 275
1- تابع $f(x) = \left\{ {\begin{array}{*{20}{l}}{(x + 1)[x]}&{|x + 1|\, < 1}\\{{x^2} + 2x}&{|x + 1|\, \ge 1}\end{array}} \right.$ در چند نقطه از اعداد حقیقی ناپیوسته است؟
2- هرگاه \[f(x) = \frac{{{{\cos }^2}x - \cos x}}{{{x^2}}}\] مقدار \[\mathop {\lim }\limits_{x \to \,0} f(2x)\] چه عددی است؟
3- اگر \[\mathop {\lim }\limits_{x \to 1} f(x) = 1\] و در یک همسایگی \[x = 1\] حاصل \[\frac{{f(x) - 1}}{{1 - x}}\] منفی باشد، نمودار f در اطراف \[x = 1\] چگونه است؟
4-
در شکل مقابل نمودار تابع f رسم شده است. حاصل $\lim_{x→۱^-}f(x+۲)+\lim_{x→۲^+}f(x-۱)$ کدام است؟
5-
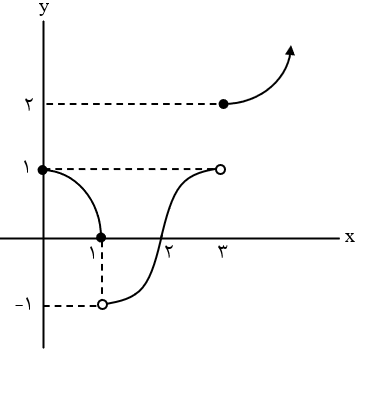
حاصل $\underset{\text{x}\to \text{ }\!\!\pi\!\!\text{ }}{\mathop{\lim }}\,\frac{{{\sin }^{۲}}\text{x}}{۱-\cos ۴\text{x}}$ کدام است؟