شرکت در آزمون آنلاین هندسه 2 - فصل سوم : روابط طولی در شکل های هندسی

1

در مثلث متساوی‌الاضلاع \[\mathop {ABC}\limits^\Delta \] به مساحت \[\frac{{9\sqrt 3 }}{4}\]، نقطۀ Dبه گونه‌ای روی ضلع BC قرار گرفته که \[\frac{{BD}}{{DC}} = \frac{1}{2}\] است. طول AD چقدر است؟

\[\sqrt {\frac{{17}}{2}} \]

\[\sqrt 8 \]

\[\sqrt 7 \]

\[\sqrt 6 \]

2

در شکل زیر طول CD کدام است ؟

\[\frac{{2\sqrt 3 }}{3}\]

\[2\]

\[4\]

\[\frac{{4\sqrt 3 }}{3}\]

3

در شکل زیر، مجموع زوایای $A\hat BC$ و $A\hat DC$ برابر با $150^\circ $ است. اگر $AC = AB = AD$، $CD = 2\sqrt 3 $ و $BC = 4$ باشد، طول AC کدام است؟

\[4\sqrt 3 \]

\[2\sqrt {13} \]

\[5\sqrt 2 \]

\[3\sqrt 6 \]

4

در شکل زیر، نسبت $\frac{m}{n}$ چقدر است؟

$\frac{۱}{{{{\sqrt ۲ }^{}}}}$

$\frac{۲}{{{{\sqrt ۲ }^{}}}}$

$\frac{۳}{{{{\sqrt ۲ }^{}}}}$

$\frac{۴}{{{{\sqrt ۲ }^{}}}}$

5

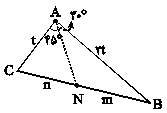
مساحت مثلث با اضلاع ۴و۶و۸ کدام است؟

$۲\sqrt{۱۵}$

$۳\sqrt{۱۵}$

$۴\sqrt{۵}$

$۶\sqrt{۵}$

شرکت در آزمون آنلاین هندسه 2 - فصل سوم : روابط طولی در شکل های هندسی | آزمون شماره 195

جست و جو

شرکت در آزمون آنلاین هندسه 2 - فصل سوم : روابط طولی در شکل های هندسی | آزمون شماره 195

جست و جو

ساخت آزمون

ساخت آزمون