شرکت در آزمون آنلاین هندسه 2 - فصل دوم : تبدیل های هندسی | آزمون شماره 24

1- فرض کنید G محل برخورد میانه‌های مثلث ABC باشد و مثلث‌های $A'B'C'$ و $A''B''C''$ به ترتیب مجانس‌های مثلث ABC با مرکز تجانس G و نسبت‌های تجانس $\frac{1}{2}$ و $ - \frac{1}{2}$ باشند، نسبت مساحت دو مثلث تبدیل یافته چقدر است؟

2- درون زاویه‌ای که از محور xها و خط d به معادله \[y = x\] ساخته می‌شود، نقطۀ \[M\,(2\,,1)\] قرار دارد. می‌خواهیم نقاط A و B را بر روی محور ox و خط d چنان پیدا کنیم که محیط مثلث MAB مینیمم گردد. طول نقطۀ A چقدر خواهد بود؟

3- در مثلث متساوی‌الاضلاع $\mathop {ABC}\limits^\Delta $ نقطۀ D در $\frac{1}{3}$ فاصلۀ AB از نقطۀ B قرار دارد و نقطۀ M بر ضلع BC واقع است. کمترین مقدار $DM + MA$ چند برابر ضلع مثلث متساوی‌الاضلاع است؟

4-

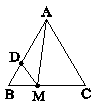
اگر بازتاب پاره‌خط $AB$ نسبت به خط $d$را $A'B'$ بنامیم، کدام گزاره در مورد چهارضلعی $\text{AA }\!\!'\!\!\text{ B }\!\!'\!\!\text{ B}$ ممکن است نادرست باشد؟

5-

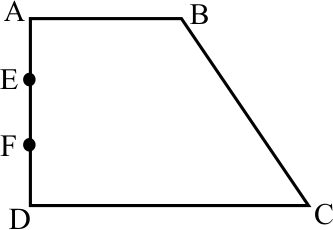
 در ذوزنقه قائم‌الزاویه شکل روبه‌رو، $DC=۲AB=۱۰$ و $\text{AD}=۱۴$ و نقاط $E$ و $F$ روی ساق $AD$ به فاصله‌ی $۶$ واحد از هم قرار دارند. کمترین مقدار $\text{FC}+\text{BE}$ کدام است؟