شرکت در آزمون آنلاین هندسه 1 - فصل سوم: چند ضلعی ها | آزمون شماره 145

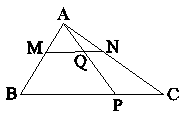
در شکل زیر، MN موازی BC و $\frac{{AM}}{{MB}} = \frac{1}{2}$ و مساحت چهار ضلعی MQPB، 24 برابر مساحت مثلث AQN است. نقطة P، ضلع BC را به چه نسبتی قطع می‌کند؟

اگر در چهارضلعی محدب ABCD وسط‌های اضلاع را به طور متوالی به هم وصل کنیم، محیط چهارضلعی پدید آمده چه رابطه‌ای با قطرهای ABCD دارد؟

کدام گزینه مثال نقض دارد؟

مطابق شکل، متوازی‌الاضلاع ABCD به مساحت 30 مفروض است. اگر بین مساحت‌های مشخص شده رابطۀ ${S_1} + {S_2} + {S_3} = 9$ برقرار باشد، مقدار ${S_2}$ کدام است؟

مساحت مثلث $\mathop {ABC}\limits^\Delta  $ برابر \[16\] است. اگر از نقطة \[M\]،‌ وسط ضلع \[BC\]، خطی موازی میانة\[BN\] رسم کنیم تا ضلع \[AC\] را در \[F\] قطع کند، مساحت چهارضلعی \[BMFN\] چقدر است؟