شرکت در آزمون آنلاین
هندسه 3
-
فصل دوم : مقاطع مخروطی
| آزمون شماره 291
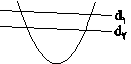
وسط وترهای ایجاد شده توسط دو خط موازی ${d_1}:y = - 2x + 5$ و ${d_2}:y = - 2x + 1$ از سهمی $y = {x^2}$ روی کدام خط قرار دارند؟
مجموع طول کوتاه‌ترین و بلندترین وتر دایرۀ ${x^2} - 4x + {y^2} - 2y = 4$ که از نقطه $A(1\,\,,\,\,1)$ می‌گذرد، کدام است؟
اگر $\left( x\text{, }\!\!~\!\!\text{ }y \right)$ نقطه‌ای روی دایره ${{x}^{۲}}+{{y}^{۲}}-۲x-۴y-۴=۰$ باشد آنگاه کمترین مقدار عبارت $\sqrt{{{(x+۲)}^{۲}}+{{(y+۲)}^{۲}}}$ کدام است؟
به مرکز هر نقطه از سهمی ${{y}^{۲}}+۲y-۸x+۹=۰$ دایره‌ای رسم می‌کنیم که از کانون سهمی بگذرد. این دایره‌ها بر کدام خط مماس‌اند؟
اگر$A\left( ۲,۱ \right)$ و ${A}'\left( ۰,۱ \right)$ دو نقطه از یک سهمی قائم باشند که کانونش بر خط $y=۲x-۱$ واقع است، مختصات کانون آن کدام است؟
