شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل دوم : هندسه | آزمون شماره 3085

اگر نقاط $A\,(1\,,\,2)$، $B\,(5\,,\,2)$، $C\,(4\,,\,0)$ و مبدأ مختصات، رئوس متوازی‌الاضلاع ABCD باشند، آنگاه حجم حاصل از دوران این چهارضلعی حول محور y چند برابر $\pi $ است؟

رئوس یک مثلث دلخواه روی یک دایره قرار دارند. مرکز این دایره بر کدام نقطه مثلث منطبق است؟

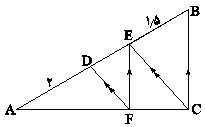
در مثلث زیر، $EF||BC$ و $DF||EC$ است. طول AB کدام است؟

در مثلث ABC داریم: $\hat A = 90^\circ $ و $AC = 15$ و $AB = 8$ در این صورت اگر AH ارتفاع رسم شده از رأس A بر ضلع BC باشد، فاصلۀ H از ضلع AC کدام است؟

در یک متوازی‌الاضلاع نقطه‌ای وجود دارد که از چهار ضلع به یک فاصله است. کدام گزینه در مورد این متوازی الاضلاع همواره درست است؟