شرکت در آزمون آنلاین
ریاضی هشتم
-
توازی و تعامد
| آزمون شماره 20485
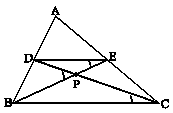
داخل مثلث $\mathop {ABC}\limits^\Delta $ خط DE را موازی ضلع BC رسم می‌کنیم. از D به C و از E به B وصل می‌کنیم تا یکدیگر را در P قطع کنند. اگر ${E_1} = 20^\circ $ و ${\hat C_1} = {10^ \circ }$ باشند، اندازة زاویه ${\hat P_1}$ کدام است؟
در شكل زير،$d||{d}`$ است. حاصل${{\hat{A}}_{2}}+{{\hat{B}}_{2}}$، كدام است؟
در شکل زیر، مثلث ABC متساوی‌الاضلاع و مثلث APQ متساوی‌الساقین است$(AQ=AP)$. اگر$AQ||BC$باشد، اندازه زاویه Q برحسب x کدام است؟
در شکل زیر، خطوط$d$ و${d}`$ با هم موازی و$AO=OD$ است. کدام گزینه ممکن است صحیح نباشد؟
