شرکت در آزمون آنلاین
هندسه 1
-
فصل سوم: چند ضلعی ها
| آزمون شماره 260
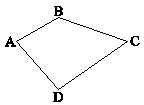
در شکل زیر، قطرهای چهارضلعی بر هم عمودند و مثلث $\mathop {BCD}\limits^\Delta $ متساوی‌الاضلاع است. اگر مساحت چهارضلعی $12\sqrt 3 $ و $AC = 8$ باشد، مساحت مثلث BCD کدام است؟
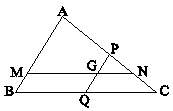
در مثلث $\mathop {ABC}\limits^\Delta $ شکل زیر، نقطۀ G مرکز ثقل مثلث است. از G خطوط PQ و MN را به ترتیب موازات AB و BC رسم کرده‌ایم. مساحت مثلث PGN چه کسری از مساحت مثلث ABC است؟
چه تعداد از گزاره‌هاي زير همواره درست هستند؟ الف) هر مستطيلي، متوازي‌الاضلاع است. ب) مستطيلي كه قطرهاي برابر داشته باشد، مربع است. ج) محل برخورد ميانه‌هاي مثلث همواره درون مثلث است. د) چهارضلعي كه قطرهايش عمود منصف هم باشند، لوزي است.
در شکل روبه‌رو رابطه‌های \[MC = t \times BC\] و \[AP = k \times AM\] برقرارند. نسبت مساحت مثلث APC به مساحت مثلث ABC کدام است؟
متوازی‌الاضلاع ABCD را در نظر بگیرید. نقطه P درون مثلث ABD را طوری انتخاب کرده‌ایم که مساحت مثلث ADP برابر 3 و مساحت مثلث PDC برابر 5 واحد باشد. مساحت مثلث PDB کدام است؟
