شرکت در آزمون آنلاین
آمار و احتمال
-
درس دوم : احتمال غیر هم شانس
| آزمون شماره 306
1- از مجموعۀ $A = \{ a\,,\,b\,,\,c\,,\,d\} $ یک زیرمجموعه به‌تصادف انتخاب می‌کنیم؛ به‌طوری که شانس انتخاب هر زیرمجموعه با تعداد اعضای آن متناسب است. احتمال آنکه زیرمجموعۀ انتخابی $\{ a\,,\,c\,,\,d\} $ باشد، چقدر است؟
2-
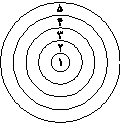
صفحۀ دارت مطابق شکل به 5 ناحیۀ مجزا تقسیم شده است. احتمال اصابت دارت به ناحیه اول برابر x و به ناحیه k ام برابر $(2k - 1)x$ است. اگر بدانیم دارت به ناحیه با شماره زوج برخورد کرده، چقدر احتمال دارد به ناحیه 2 برخورد کرده باشد؟
3- چهار بازیکن با شماره‌های 2، 4 ، 6 و 8 در یک بازی رقابت می‌کنند که در پایان تنها یک نفر برنده می‌شود، احتمال برنده شدن هر کدام از بازیکنان متناسب است با مربع شمارۀ او. احتمال برنده شدن بازیکن شمارۀ 8 چقدر بیشتر از احتمال برنده شدن بازیکن شمارۀ 6 است؟
4- از بین اعداد طبیعی عددی را به تصادف انتخاب می‌کنیم. اگر احتمال ظاهر شدن یک عدد k رقمی برابر ${x^k}$ باشد، احتمال ظاهر شدن یک عدد تک رقمی چقدر است؟
5- در یک تاس ناسالم، احتمال آمدن اعداد زوج k برابر احتمال آمدن اعداد فرد است. اگر در پرتاب این تاس، احتمال رو شدن عددی بزرگ‌تر از 3، ${1_/}8$ برابر احتمال رو شدن عددی کوچک‌تر از 3 باشد، احتمال رو شدن عدد 3 در پرتاب این تاس کدام است؟