شرکت در آزمون آنلاین هندسه 2 - فصل سوم : روابط طولی در شکل های هندسی | آزمون شماره 33

با معلومات $BC = 6\sqrt 3 $ و $AC = 6$ و $\hat B = 60$ چند مثلث با رأس‌های \[A\]، \[B\] و \[C\] می‌توان ساخت؟  

مساحت مثلثی سه برابر محیط آن است. حاصل $\frac{1}{{{r_a}}} + \frac{1}{{{r_b}}} + \frac{1}{{{r_c}}}$ در آن مثلث کدام است؟ (${r_a}$، ${r_b}$ و ${r_c}$ به‌ترتیب شعاع دایره‌های محاطی خارجی اضلاع a و b و c هستند.)

در مثلث قائم الزاویه $(A = {90^ \circ })\,ABC$ دو نقطۀ E و F را به ترتیب روی AB و AC به گونه‌ای انتخاب می‌کنیم که نیم‌سازهای زاویه‌های $E\hat FC$ و $F\hat EB$ یکدیگر را در نقطه P روی وتر قطع کنند. اگر $BP = 6$ و $CP = 8$ باشد حاصل $|AB - AC|$ چقدر است؟

 در مثلث $ABC$ داریم: $\hat{A}=۱۲۰{}^\circ ~,~AB=\sqrt{۲}-۱~,~AC=\sqrt{۲}+۱$. طول ضلع $BC$ کدام است؟

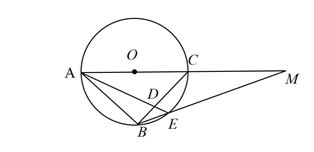
مطابق شكل در دایره‌ای به شعاع ۲واحد، داریم:$\text{ }\!\!~\!\!\text{ }{{۴۵}^{\circ }}$ = $\hat{M}$ و $\widehat{AB}={{۱۲۰}^{\circ }}$ ، طول پاره خط $BD$ کدام است؟