شرکت در آزمون آنلاین
ریاضی هشتم
-
فصل ششم : مثلث
| آزمون شماره 13718
1-
مثلث ABC در راس A قائمه است و AD نیمساز زاویه A است . اگر \[\mathop C\limits^ \wedge = {40^ \circ }\] باشد ، اندازه زاویه ADB چند درجه است ؟
2- اگر $A = {x^2} - 3$ و $B = {x^3} + 2x - 7$ باشند، مقدار عددی عبارت ${A^2} - Bx$ به ازای $x = - 3$ چه عددی خواهد شد؟
3-
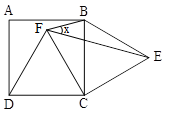
چهارضلعی ABCD مربع است و دو مثلث \[\mathop {BEC}\limits^\Delta \] و \[\mathop {FDC}\limits^\Delta \] متساوی‌الاضلاع هستند. اندازة زاویة x کدام است؟
4- مثلث قائم‌الزاویه‌ای دارای محور تقارن است. اگر طول وتر آن 10 سانتی‌متر باشد، مساحت مثلث کدام است؟
5-
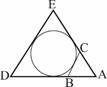
در شکل محیط مثلث \[\mathop {ADE}\limits^\Delta \]برابر\[50\,cm\]و طول\[\overline {DE} \] برابر\[15\,cm\] است. محیط مثلث\[\overline {ABC} \] را حساب کنید.
