شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 2466
1- اگر $a = \frac{b}{2} = \frac{c}{3} = \frac{d}{{4 + b}}$ باشد، کمترین مقدار $a + b + c + d$ کدام است؟
2-
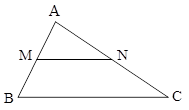
در شکل مقابل \[BC||MN\] است و مساحت ذوزنقه MNCB هشت برابر مساحت مثلث AMN می‌باشد. نسبت میانه‌های نظیر رأس A در مثلث‌های AMN و ABC کدام است؟
3- در مستطیل ABCD، نقطة M روی ضلع AB به اندازه a طوری قرار گرفته است که این ضلع را به نسبت 4 و 5 قطع می‌کند و نیز پاره‌خط‌های MC و MD برهم عمودند. مقدار\[MC + MD\]کدام است؟
4- اگر داشته باشیم \[\frac{{{a_1}}}{1} = \frac{{{a_2}}}{2} = \frac{{{a_3}}}{3} = ... = \frac{{{a_n}}}{n}\] آنگاه حاصل عبارت \[\frac{{{a_1} + {a_2} + {a_3} + ... + {a_n}}}{{{a_5}}}\] کدام است؟
5- در مثلث قائم الزاویه \[A\mathop B\limits^\Delta C\]از وسط ضلع AC عمودی بر وتر BC رسم نموده‌ایم و 4=HC و 9=BC طول ضلع AB چقدر است؟