 شرکت در آزمون آنلاین
هندسه 1
-
هندسه 1
| آزمون شماره 5003
شرکت در آزمون آنلاین
هندسه 1
-
هندسه 1
| آزمون شماره 5003
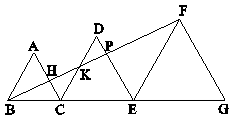
در شکل زیر، سه مثلث متساویالاضلاع به اضلاع 3، 4 و 5 در کنار هم قرار دارند. نسبت مساحت مثلث $\mathop {DKP}\limits^\Delta $ به مساحت مثلث $\mathop {PEF}\limits^\Delta $ کدام است؟
در مثلث قائم الزاویه $ABC$،$\hat{B} = ۹۰ $ و AD نیم ساز زاویه A بوده و $BD=۱$ و $CD=۲$ واحد می باشد. در صورتی که از نقطه $D$عمود $DH$ را بر ضلع$AC$رسم نماییم، طول پاه خط$BH$ کدام است؟
در مثلث متساویالساقین $ABC$ $(AB=AC)$، از نقطهی $O$ روی قاعده $BC$ پارهخط $OE$ به موازات ساق $AC$ و پارهخط $OF$ به موازات ساق $AB$ رسم شده است. طول مجموع این دو پارهخط با طول کدام یک برابر است؟


