شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل سوم : توابع

تابع $f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{1}{x}}&{x \ge 2}\\{a - x}&{x < 2}\end{array}} \right.$ یک به یک است. حدود a کدام است؟

$a \ge \frac{۱}{۲}$

$a \le \frac{۱}{۲}$

$a \ge \frac{۵}{۲}$

$a \le \frac{۵}{۲}$

نمودار تابع $f(x) = - 2{x^2} + x + 30$ را دو واحد به طرف xهای منفی و سپس یک واحد به طرفyهای مثبت انتقال می‌دهیم. نمودار جدید در کدام بازه، بالای خط $y = x + 1$ است؟

$( - ۴\,,\,۳)$

$( - ۳\,,\,۴)$

$ ۲) $( - ۳\,,\,

$ ۳) $( - ۶\,,\,۲)$ ۴) $( - ۲\,,\,۶)$

اگر تابع با ضابطة $f(x) = \left\{ \begin{array}{l}{x^2} - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x \ge 2\\ax - 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,x < 2\end{array} \right.$ معكوس‌پذير باشد، حداكثر مقدار ممكن براي a كدام است؟

اگر $f=\left\{ \left( -۱,۳ \right),\left( ۱,۲ \right),\left( ۲,۱ \right) \right\}$ و $g\left( x \right)=\sqrt{۳x-{{x}^{۲}}}$ آنگاه تابع $h=\frac{{{g}^{۲}}+f}{۲-f}$ کدام است؟

$~\left\{ \left( ۲,۳ \right) \right\}$

$~\left\{ \left( -۱,-۳ \right),\left( ۲,۳ \right) \right\}$

$~\left\{ \left( -۱,۳ \right),\left( ۲,۳ \right) \right\}$

$\varnothing $

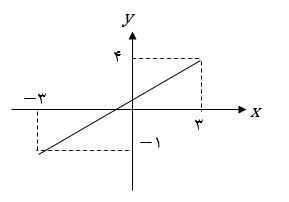
نمودار تابع $y=f\left( x \right)$ به صورت زیر است. کدام نمودار تابع $y=\left| x \right|$ را در نقاط بیشتری قطع می‌کند؟