شرکت در آزمون آنلاین ریاضی 3 و پایه - فصل چهارم: مشتق | آزمون شماره 376

1- تعداد نقاط مشتق‌ناپذیری تابع f با ضابطۀ $f(x) = \,|({x^3} - x){({x^2} - 5x + 4)^2}|$ کدام است؟

2-

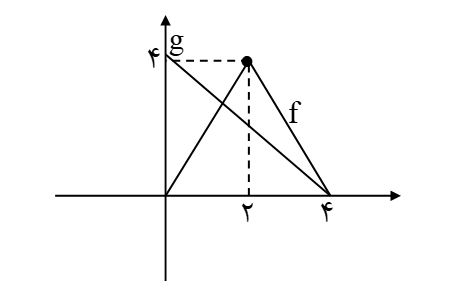
نمودار تابع f و g به صورت مقابل هستند. اگر $k(x)=\frac{g(x)}{f(x)}$ باشد، حاصل $k'(۳)$ کدام است ؟

3-

اگر رابطه ${f}'\left( x \right)\left( {{x}^{۲}}+۱ \right)-۲xf\left( x \right)=۲{{x}^{۵}}+۴{{x}^{۳}}+۲x$ برقرار باشد کدام رابطه بین توابع $f$و $g$ می‌تواند برقرار باشد؟

4-

تابع $\text{f}\left( \text{x} \right)=\left\{ \text{ }\!\!~\!\!\text{ }\begin{matrix} {{\text{x}}^{۲}}+۳\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!~~~~~~~~\text{ x}\ge ۱ \\ ۲\text{x}+۲\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!~~~~~~~\text{ x}<۱ \\\end{matrix} \right.$ از نظر پیوستگی و مشتق‌پذیری در $\text{x}=۱$ چگونه است؟

5-

اگر $f\left( x \right)=x\left[ \cos x+۲ \right]$ و$g\left( x \right)={{x}^{۲}}+۳x$ باشد، حاصل${{\left( gof \right)}^{\acute{\ }}}\left( ۰ \right)$ کدام است؟