شرکت در آزمون آنلاین
هندسه 3
-
فصل سوم : بردارها
| آزمون شماره 26
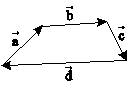
در شکل زیر، چهار بردار $\vec a$، $\vec b$، $\vec c$ و $\vec d$، اضلاع یک چهارضلعی هستند. اگر بین سه بردار واحد $\vec a$، $\vec b$ و $\vec c$، رابطۀ $\vec a\,.\,\vec b + \vec a\,.\,\vec c + \vec b\,.\,\vec c = \frac{{1 + \sqrt 3 }}{2}$ برقرار باشد، مجموع مربعات طول اضلاع این چهارضلعی کدام است؟
اگر نقاط $A(1\,,\,2\,,\,3)$، $B(2\,,\,3\,,\, - 1)$ و $D( - 2\,,\, - 1\,,\,5)$ رئوس متوازیالاضلاع ABCD باشند، طول قطر AC کدام است؟
اگر نقاط $A\left ( ۲,-۱,۳ \right )$ و $B\left ( ۳,۲,۰ \right )$ و $C\left (a,b,۶ \right )$ روی یک خط راست باشند ab کدام است؟
بین سه بردار $\vec{a}$ و $\vec{b}$ و $\vec{c}$ رابطهی $\vec{a}\times \left( \vec{b}+\vec{c} \right)-\vec{b}\times \vec{c}=\vec{i}\times \left( \vec{j}\times \vec{k} \right)$ برقرار است. بردارهای $\vec{a}$ و $\vec{b}$ و $\vec{c}$ چه وضعیتی نسبت به هم دارند؟
اگر $\vec{a}=\left( ۱,۰,-۲ \right)$ و $\vec{a}+۲\vec{b}-۳\vec{c}=\left( ۱,۲,۳ \right)$،آنگاه $۲\vec{a}.\vec{b}$ چند واحد از $۳\vec{a}.\vec{c}$ کمتر است؟
