شرکت در آزمون آنلاین
هندسه 2
-
فصل دوم : تبدیل های هندسی
| آزمون شماره 562
نقاط O و M به فاصلۀ 2 واحد از هم مفروض‌اند. اگر مجانس نقطة M به مرکز تجانس O و با نسبت تجانس 3، نقطة \[M'\] باشد، آنگاه مجانس \[M'\] به مرکز تجانس M و نسبت تجانس \[ - 4\]، چه فاصله‌ای از نقطة O دارد؟
در اثر یک تجانس معکوس انبساطی خط \[\Delta \] به \[\Delta '\] تصویر شده است. کدام‌یک از نقطه‌های زیر می‌تواند مرکز این تجانس باشد؟
شکل مقابل، شش ضلعی ای را نشان می دهد که در آن همه اضلاع با هم برابرند $\hat{D}=\hat{E}=\hat{F}=۱۲۰^{\circ}, \hat{A}=\hat{C}=۶۰^{\circ}$ اگر بخواهیم با جابجا کردن رئوس، این شش ضلعی را به شکل بسته دیگری با همین اضلاع تبدیل کنیم، مساحت شکل حداکثر چند درصد افزایش می یابد؟
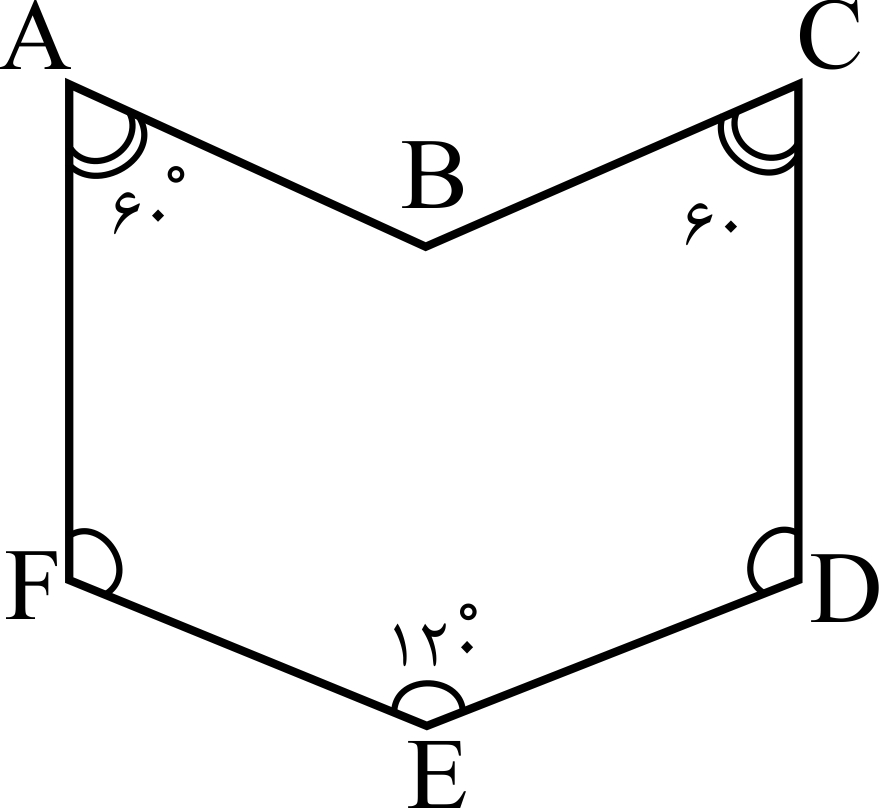
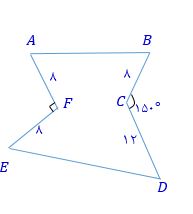
در شکل مقابل اگر بدون تغییر محیط و تعداد اضلاع، مساحت شکل را به کمک بازتاب افزایش دهیم، میزان افرایش مساحت کدام است؟
نقطه M درون زاویه xOy است. می‌خواهیم نقاط A و B را بر اضلاع Ox و Oy چنان انتخاب کنیم که محیط مثلث MAB مینیمم باشد. برای این کار از تبدیل ........... به تعداد ........... استفاده می‌کنیم.