شرکت در آزمون آنلاین
ریاضی 3 و پایه
-
فصل چهارم: مشتق
| آزمون شماره 48
1-
اگر $g(x)=x+\sqrt{x}$ و $\underset{x\to ۲}{\mathop{\lim }}\,\frac{f(x)-f(۲)}{x-۲}=\frac{۴}{۳}$ باشد، حاصل مشتق تابع $y=(fog)(x)+f(۲x)$ به ازای $x=۱$ کدام است؟
2-
اگر $f(x)= \begin{cases}۲ x+۱ & x \geqslant ۱ \\ x^۳+ x^{۲} & x<۱\end{cases}$، حاصل $\underset{\text{h}\to {{۰}^{-}}}{\mathop{\lim }}\,\frac{\text{f}\left( ۱ \right)-\text{f}\left( ۱-\text{h} \right)}{\text{h}}$ کدام است؟
3-
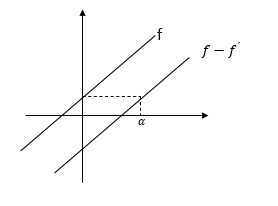
نمودار توابع f و$f-{f}'$ به صورت مقابل است. مقدار $\alpha $ کدام است؟
4-
تابع $f\left( x \right)=\left( ax+۳ \right)\left| x+b \right|$ مفروض است، اگر $f_{+}^{'}\left( ۲ \right)-f_{-}^{'}\left( ۲ \right)=۳$ باشد، مقدار a کدام است؟
5-
اگر $f(x)=\frac{۲(x-۳)\cos^۲(۲\pi x)}{۲^x-۲x-۱}$ باشد، آنگاه$ f'(۳)$ کدام است؟