شرکت در آزمون آنلاین
هندسه 2
-
فصل سوم : روابط طولی در شکل های هندسی
| آزمون شماره 271
در مثلث قائمالزاویه \[(\mathop A\limits^ \wedge = {90^ \circ })ABC\] به اضلاع قائم 6 و 8 واحد، نیمساز زاویۀ C (کوچکترین زاویۀ داخلی مثلث)، نیمساز بزرگترین زاویۀ داخلی مثلث را در نقطۀ O قطع میکند. نسبت مساحت دو مثلثی که در طرفین OC ایجاد میشود و OC یکی از اضلاع آنها است، چقدر است؟
در مثلث \[A\mathop B\limits^\Delta C\] میانة AM را رسم میکنیم. نیمسازهای زوایای \[A\hat MB\] و \[A\hat MC\] اضلاع AB و AC را به ترتیب در P و Q قطع میکنند و O محل تلاقی AM و PQ است. کدام گزینه الزاماً صحیح نیست؟
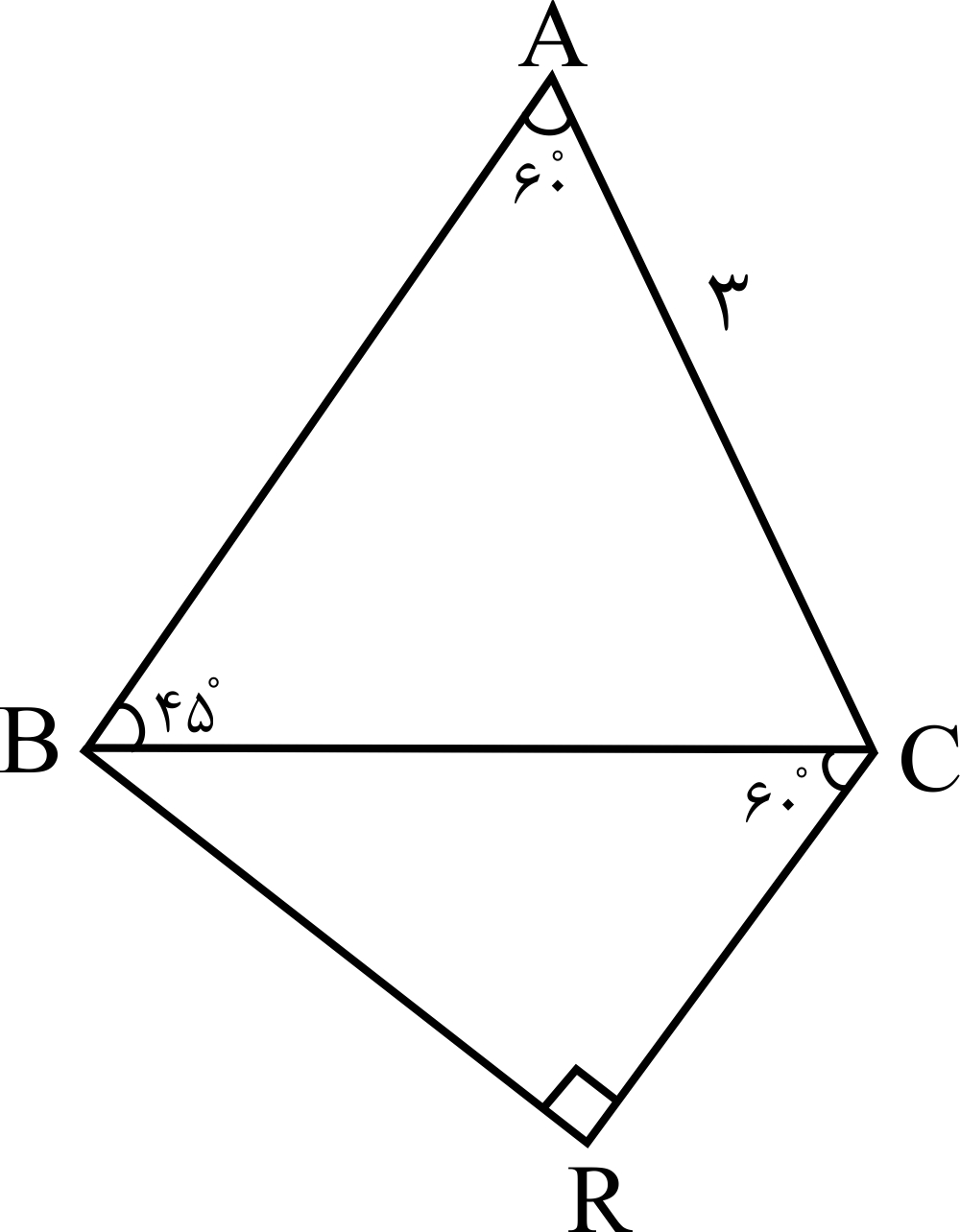
طول پارهخط $CR$ چند واحد است؟
در مثلثABC، $\hat{A}=۴۵^{\circ} , \hat{B}= ۱۰۵^{\circ}$ و طول ضلع C برابر با $\sqrt{۸}$ است و اندازه ضلع a کدام است؟
در مثلث $ABC$ روابط $\frac{{{b}^{۴}}+{{c}^{۴}}-{{a}^{۴}}}{\sqrt{۳}a-bc}=۲bc$ و ${{a}^{۲}}+{{b}^{۲}}+{{c}^{۲}}=۲$ بین اضلاع برقرار است. سینوس زاویۀ $\hat{A}$ کدام است؟
