شرکت در آزمون آنلاین حسابان 1 - فصل پنجم : حد و پیوستگی

اگر تابع $f(x) = \left\{ \begin{array}{l}ax + [x]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x > 2\\[\frac{x}{3}] + b\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 2\\3\cos (x - 2)\,\,\,\,\,\,\,\,x < 2\end{array} \right.$ در نقطۀ $x = 2$ پیوسته باشد، حاصل $a - b$ کدام است؟

$\frac{۵}{۲}$

$\frac{۳}{۲}$

$ - \frac{۵}{۲}$

$ - \frac{۳}{۲}$

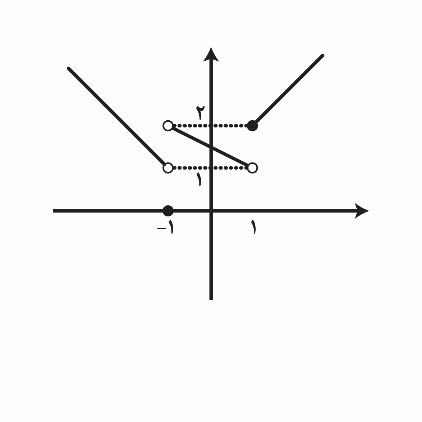
با توجه نمودار تابع $f$ ،حاصل عبارت $\underset{x\to {{۱}^{-}}}{\mathop{\lim }}\,f\left( x \right)-\underset{x\to -{{۱}^{+}}}{\mathop{\lim }}\,f\left( x \right)$کدام است؟