شرکت در آزمون آنلاین ریاضی 3 و پایه - فصل پنجم: کاربرد مشتق | آزمون شماره 105

1- نمودار تابع $y = {x^3} - \frac{3}{2}{x^2} - 6x$ به صورت زیر است. مجموع مقادیر m که به‌ازای آن معادلۀ ${x^3} = \frac{3}{2}x + 6x + m$، 2 ریشۀ متمایز دارد، کدام است؟

2- برد تابع \[f(x) = {x^3} + 2x - 5\] در بازۀ \[[ - 2,1]\] کدام است؟

3-

اگر $x=-۲$ طول نقطه مینیمم نسبی تابع $f\left( x \right)=x-\sqrt{a-{{x}^{۲}}}$ باشد، ماکزیمم مطلق تابع روی دامنه‌اش کدام است؟

4-

 تابع $f\left( x \right)=x+\frac{۱}{x}$ مفروض است. در کدام بازه $f$ اکیداً صعودی و $f^{'} $ اکیداً نزولی است؟

5-

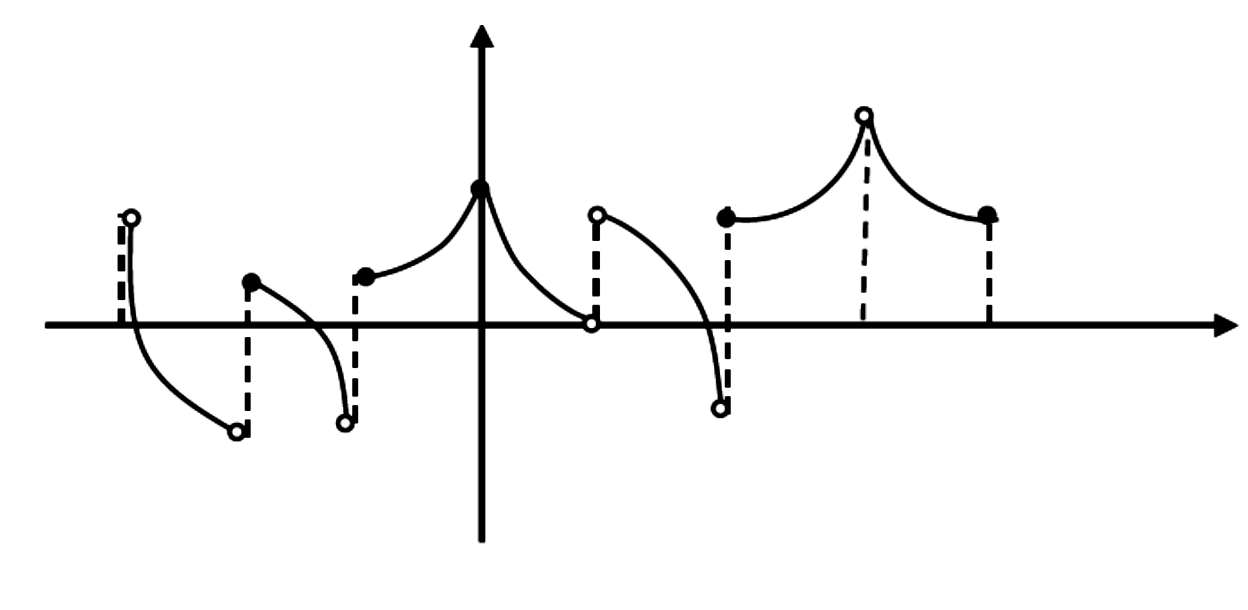
اگر شکل مقابل نمودار تابع $y=f(x)$ باشد، تعداد نقاط اکسترمم های نسبی تابع f کدام است؟