شرکت در آزمون آنلاین
هندسه 1
-
فصل سوم: چند ضلعی ها
| آزمون شماره 365
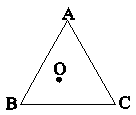
در مثلث متساوی‌الاضلاع ABC با مساحت $3\sqrt 3 $، اگر مجموع فواصل نقطۀ O از دو ضلع AB و BC برابر یک واحد باشد، مساحت مثلث AOC کدام است؟
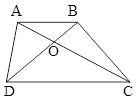
در ذوزنقۀ شکل زیر، و است. در این صورت مساحت این ذوزنقه چقدر است؟
در مثلث ABC با اضلاع a، b و c داریم $\frac{{b{h_a} + c{h_b} + a{h_c}}}{{\frac{b}{a} + \frac{c}{b} + \frac{a}{c}}} = 20$. مساحت مثلث کدام است؟
با توجه به شکل$M$ وسط$BC$ است و$\frac{{AD}}{{DB}} = \frac{3}{2}$ اگر مجموع اندازه‌های$MN$ و$BC$ برابر 24 باشد، اندازۀ$AM$ کدام است؟
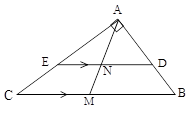
نقطه دلخواه P واقع بر امتداد ضلع BC را به راس A وصل می‌کنیم. از M (وسط BC) خطی به موازات AP رسم می‌کنیم تا AC را در N قطع کند. نسبت مساحت مثلث ABC به مثلث PNC کدام است؟