شرکت در آزمون آنلاین
هندسه 1
-
فصل اول: ترسیم های هندسی و استدلال
| آزمون شماره 5347
شرکت در آزمون آنلاین
هندسه 1
-
فصل اول: ترسیم های هندسی و استدلال
| آزمون شماره 5347
در مثلث نقاط D و E بهترتيب روي AC و AB قرار دارند؛ بهطوري كه $E\hat CB = 30^\circ $ و $D\hat BC = 2A\hat BD = 2A\hat CE = 40^\circ $. اگر محل برخورد $CE$ و $BD$ را F بناميم، زاوية $F\hat AD$ چند درجه است؟
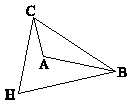
در شکل زیر، H محل برخورد ارتفاعهای مثلث است. اگر $B\hat HC = {68^ \circ }$ باشد، زاویة A چند درجه است؟
چند قضیه از بین قضیه های مطرح شده دو شرطی هستند؟
الف) $a< b\rightarrow a^{۲}< b^{۲}$
ب) $a=b\rightarrow cosa= cosb$
پ) $a=b\rightarrow \left [ a \right ]=\left [ b \right ] $
ت) $a=b\rightarrow a^{۳}=b^{۳}$
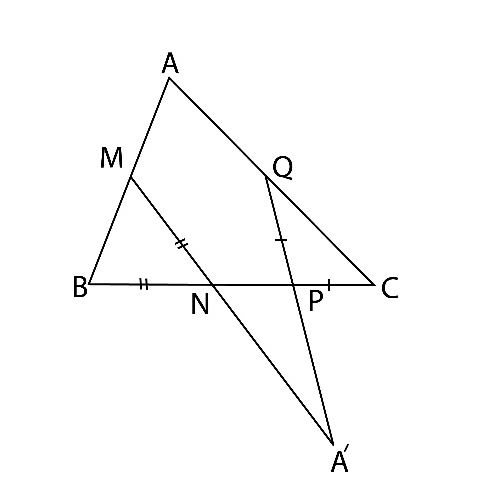
در شکل زیر داریم: $BN=NM$ و $CP=PQ\text{ }\!\!~\!\!\text{ }$ ، اگر $\hat{A}=۷۰{}^\circ $ باشد. آنگاه زاویه $A'$ چند درجه است؟