شرکت در آزمون آنلاین
حسابان (2)
-
فصل ٤: مشتق
| آزمون شماره 333
1- اگر f در \[x = 2\] مشتق‌پذیر باشد، به طوری‌که \[\mathop {\lim }\limits_{h \to 0} \frac{{f(2 - h) - 3}}{h} = 3\] مشتق \[y = \frac{1}{x}f(2x)\] به‌ازای \[x = 1\] چه عددی است؟
2-
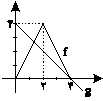
نمودار توابع f و g به صورت مقابل است. حاصل مشتق تابع $y = \frac{{x + f(x)}}{{x - g(x)}}$ در نقطة $x = 3$ چقدر است؟
3- با فرض $f(x) = \frac{{3x - 1}}{{\sqrt {x + 1} }}$ حاصل $\mathop {\lim }\limits_{h \to 0} \frac{{f(3 - h) - 4}}{h}$ کدام است؟
4- اگر $xf(2x - 1) = 3g(2 - 3x)$ به طوری که $f'(3) = 0$ مقدار $\frac{{f''(3)}}{{g''( - 4)}}$ چه عددی است؟
5- تابع f در $x = 2$ مشتق‌پذیر و $\mathop {\lim }\limits_{h \to 0} \frac{{f(2 - h) - 3}}{h} = 4$ است. مقدار مشتق تابع $y = {f^2}(\frac{4}{x})$ در نقطۀ $x = 2$ چقدر است؟