شرکت در آزمون آنلاین
هندسه 3
-
فصل سوم : بردارها
| آزمون شماره 184
مساحت متوازی‌الاضلاعی که دو قطر آن روی بردارهای $3\vec a + 4\vec b$ و $2\vec a - \vec b$ قرار دارند، چند برابر مساحت مثلثی است که دو ضلع آن روی بردارهای $\vec a + 2\vec b$ و $2\vec a + 2\vec b$ قرار دارند؟
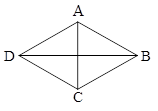
در لوزی داده شده مطابق شکل اگر $\left| {\overrightarrow {AD} } \right| = 3$ و $\left| {\overrightarrow {AC} } \right| = 3$ باشد، حاصل $\overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AB} $ کدام است؟
اگر نقاط $A\left ( m,۰,۰ \right )$ و $B\left ( ۰,m,۰ \right )$ و $C\left ( ۰,۰,m \right )$ سه راس مثلث ABC بوده و نقطه H محل تلاقی ارتفاع های این مثلث باشد. حاصل $A\vec{H}+B\vec{H}+C\vec{H}$ کدام است؟
اگر دو بردارهای غیر صفر و غیر موازی $\overset{\scriptscriptstyle\rightharpoonup}{a}$ و $\overset{\scriptscriptstyle\rightharpoonup}{b}$ مفروض باشند و $\overset{\scriptscriptstyle\rightharpoonup}{u}=۳\overset{\scriptscriptstyle\rightharpoonup}{a}+x\overset{\scriptscriptstyle\rightharpoonup}{b}$ و $\overset{\scriptscriptstyle\rightharpoonup}{v}=\left( ۱-x \right)\overset{\scriptscriptstyle\rightharpoonup}{a}-\frac{۲}{۳}\overset{\scriptscriptstyle\rightharpoonup}{b}$ موازی و هم جهت باشند x کدام است؟
در مثلث ABC داریم: $۳\overrightarrow{AB}.\overrightarrow{AC}=\left| \overrightarrow{BA}\times \overrightarrow{BC} \right|$ . در این صورت کسینوس زاویه A کدام است؟
