شرکت در آزمون آنلاین
هندسه 1
-
فصل سوم: چند ضلعی ها
| آزمون شماره 605
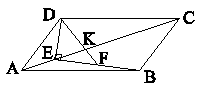
در متوازی‌الاضلاع ABCD، $EF = FB$ و DE بر BE عمود است. اگر $EC = 14$، $DE = 6$ و $AE = 4$ مساحت مثلث EFK کدام است؟
مساحت دایرۀ محیطی مثلث ABC با رئوس \[A(1,1)\] و \[B( - 1,1)\] و \[C(2, - 1)\] چند برابر \[\pi \] است؟
نقطة M درون مثلث متساوی‌الاضلاعی به مساحت $\frac{{16}}{{\sqrt 3 }}$مفروض است. اگر M از دو ضلع مثلث به فاصلة 1 و 2 واحد باشد، از ضلع سوم به چه فاصله‌ای است؟
اگر وسط‌های اضلاع هر چهارضلعی را به طور متوالی به هم وصل کنیم، یک متوازی‌الاضلاع پدید می‌آید، در چه صورتی این چهارضلعی یک مستطیل می‌شود؟
چهار نقطۀ $A\,(2\,,\,2)$ و $B\,(3\,,\,6)$ و $C\,(6\,,\,5)$ و $D\,(8\,,\,1)$ مفروض است. مساحت چهارضلعی ABCD کدام است؟