 شرکت در آزمون آنلاین
حسابان 1
-
فصل سوم : تابع نمایی و لگاریتمی
| آزمون شماره 387
شرکت در آزمون آنلاین
حسابان 1
-
فصل سوم : تابع نمایی و لگاریتمی
| آزمون شماره 387
نمودار تابع $f(x) = {3^{ax + b}}$ نمودار تابع $g(x) = {x^2}$ را در دو نقطه با طول $x = 1$ و $x = 3$ قطع میکند. نمودار ${f^{ - 1}}(x)$ خط $y = 1$ را با کدام طول قطع میکند؟
اگر ضابطة وارون $y = {4^x} + {2^{x + 1}}$ بهصورت $y = {\log _4}f(x)$ باشد، $f(8)$ چه عددي است؟
اگر $|{\log _2}x + 1|\,\, < 2$ باشد، آنگاه $[x]$ چند مقدار مختلف میتواند داشته باشد؟
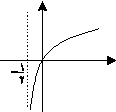
نمودار تابع $f(x) = a + {\log _2}(2x + b)$ به صورت مقابل است. حاصل ${f^{ - 1}}({\log _2}5)$ کدام است؟
حاصل $\frac{۱}{۴}{{\left( log_{\sqrt{۲۱}}^{۷} \right)}^{۲}}+\left( log_{\sqrt{۲۱}}^{\sqrt{۳}} \right)\left( log_{۲۱}^{۱۴۷} \right)$ کدام است؟


