شرکت در آزمون آنلاین هندسه 1 - فصل دوم: تالس و تشابه

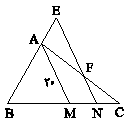
1- در مثلث با طول ميانۀ $AM = 20$، نقطۀ N بر روی BC را چنان انتخاب می‌کنیم که $\frac{{CN}}{{BN}} = \frac{3}{4}$ و از نقطۀ N خطی موازی AM می‌کشیم تا AC را در F و امتداد AB را در E قطع کند. طول پاره‌خط EF کدام است؟

$\frac{{۴۰}}{۷}$

$\frac{{۴۵}}{۷}$

$\frac{{۴۸}}{۷}$

$\frac{{۵۰}}{۷}$

2- در مثلث $\mathop {ABC}\limits^\Delta $، نقطه D روی ضلع AB چنان قرار گرفته است که \[2AD = 3DB\]. از نقطه D خطی موازی BC می‌کشیم تا ضلع AC را در E قطع کند. مساحت مثلث $\mathop {EBC}\limits^{} $ چند برابر مساحت مثلث $\mathop {EBD}\limits^\Delta $ است؟

$\frac{۵}{۳}$

$\frac{۳}{۲}$

$\frac{۵}{۲}$

$\frac{۲}{۳}$

3- در ذوزنقة ABCD مطابق شکل، حاصل \[2z + t\] کدام است؟

\[\frac{{15}}{4}\]

\[6\]

\[\frac{{21}}{4}\]

\[\frac{{25}}{4}\]

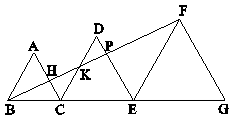
4- در شکل زیر، سه مثلث متساوی‌الاضلاع به اضلاع 3، 4 و 5 در کنار هم قرار دارند. نسبت مساحت مثلث $\mathop {DKP}\limits^\Delta $ به مساحت مثلث $\mathop {PEF}\limits^\Delta $ کدام است؟