شرکت در آزمون آنلاین هندسه 1 - فصل سوم: چند ضلعی ها | آزمون شماره 608

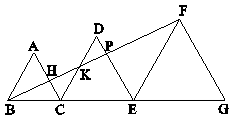
1- در شکل زیر، سه مثلث متساوی‌الاضلاع به اضلاع 3، 4 و 5 در کنار هم قرار دارند. نسبت مساحت مثلث $\mathop {DKP}\limits^\Delta $ به مساحت مثلث $\mathop {PEF}\limits^\Delta $ کدام است؟

2- چه تعداد از گزینه‌های زیر قضیۀ دو شرطی می‌باشند؟ الف) مثلثی که هیچ دو ارتفاعش برابر نباشند، متساوی‌الساقین نمی‌باشد. ب) در هر مثلث، مجموع هر دو ضلع از ضلع سوم بزرگ‌تر است. ج) در مربع، قطرها برابر و برهم عمودند.

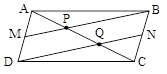
3- در متوازی‌الاضلاع$ABCD$،$M$ و$N$ به‌ترتیب وسط‌های ضلع‌های$AD$ و$BC$ هستند. اگر$AC + PQ = 36$ باشد. اندازۀ$AQ$ کدام است؟

4- روی اضلاع یک متوازی‌الاضلاع نقاط$M$ و$N$ و$K$ و$L$ را طوری انتخاب می‌کنیم که$AM = BN = CK = DL$ باشد، دو قطر چهار ضلعی$MNKL$ همواره:

5- در ذوزنقۀ شکل زیر M وسط ساق و MN عمود بر ساق AD است. اگر $\frac{3}{4}DN = 3NA = NM = 6$ باشد، مساحت ذوزنقه چقدر است؟