شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 2033
1-
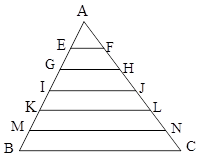
در مثلث ، پاره‌خط‌هایی به موازات ضلع BC رسم کرده‌ایم؛ به‌طوری که ضلع AB را به شش قسمت مساوی تقسیم کرده‌اند. اگر $KL = {3_/}2$ باشد، طول پاره‌خط BC چقدر است؟
2- روی پاره‌خط AB به طول 14 واحد نقاط P و Q را به گونه‌ای انتخاب کرده‌ایم که \[\frac{{QA}}{{PA}} = \frac{{PB}}{{QB}} = \frac{5}{2}\] است. طول PQ چقدر است؟
3- در شکل مقابل\[MN||PB||CL\]و\[MP||BC\]می‌باشد. حاصل\[x + y\] کدام است؟ \[(PB = y{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} CP = x)\]
4- در شکل مقابل اگر \[AB = 3\] و \[BD = 9\] آنگاه اندازة AC برابر کدام است؟
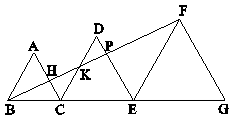
5-
در شکل زیر، سه مثلث متساوی‌الاضلاع به اضلاع 3، 4 و 5 در کنار هم قرار دارند. نسبت مساحت مثلث $\mathop {DKP}\limits^\Delta $ به مساحت مثلث $\mathop {PEF}\limits^\Delta $ کدام است؟
