شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل سوم : توابع
| آزمون شماره 487
تابع f با ضابطۀ $f(x) = 4x - \frac{1}{x}$ با دامنۀ $( - \infty \,,\,0)$ را در نظر بگیرید. نمودار تابع ${f^{ - 1}}$ خط $y = x + 2$ را در نقطه‌ای با کدام طول قطع می‌کند؟
دامنة توابع $f(x) = \frac{x}{{|x - 1| - 2}}$ و $g(x) = \frac{{{x^2} + 1}}{{{x^2} + ax + b}}$ یکسان است. حاصل ${a^2} - {b^2}$ کدام است؟
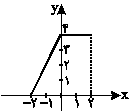
نمودار تابع $y = f(x)$ به صورت مقابل است. طول قسمتی از نمودار $y = - \frac{1}{2}f(x + 1)$ که در ناحیه سوم قرار دارد کدام است؟
اگر $\left[ a \right]!+\left[ b \right]!=۱۲۶$ باشد، حاصل $\left( ۴\left[ \frac{a+b}{۵} \right] \right)!$ کدام است؟ ($\left[ {} \right]$ نماد جزء صحیح است)
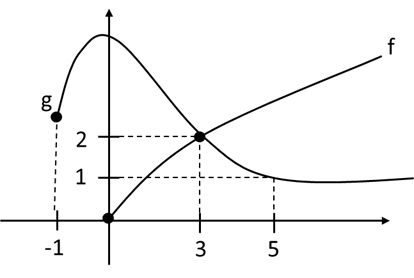
*نیازمند اصلاح در تصویر سوال: تابع g تا ۵ باید رسم شود و با دایره توپر*
اگر $f , g$ به شکل مقابل باشند، دامنه تابع $h\left( x \right)=\frac{f\left( x \right)+g\left( x \right)}{\sqrt{f\left( x \right)-۲}}$ کدام است؟
