شرکت در آزمون آنلاین
هندسه 1
-
فصل سوم: چند ضلعی ها
| آزمون شماره 395
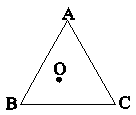
در مثلث متساوی‌الاضلاع ABC با مساحت $3\sqrt 3 $، اگر مجموع فواصل نقطۀ O از دو ضلع AB و BC برابر یک واحد باشد، مساحت مثلث AOC کدام است؟
اگر وسط‌های اضلاع یک ......... را متوالیاً به هم وصل کنیم، یک ......... تشکیل می‌شود.
در ذوزنقه‌ای با طول قاعده‌های 4 و 6 واحد و ارتفاع 5 واحد قطرها را رسم می‌کنیم. مساحت کوچک‌ترین مثلث ایجاد شده کدام است؟
چه تعداد از گزاره‌هاي زير همواره درست هستند؟ الف) هر مستطيلي، متوازي‌الاضلاع است. ب) مستطيلي كه قطرهاي برابر داشته باشد، مربع است. ج) محل برخورد ميانه‌هاي مثلث همواره درون مثلث است. د) چهارضلعي كه قطرهايش عمود منصف هم باشند، لوزي است.
اگر تعداد قطرهای رسم شده از یک رأس n ضلعی، \[{n^2} - 8n + 5\] باشد، مجموع زوایای داخلی آن چندضلعی چند برابر (90 است؟