شرکت در آزمون آنلاین
ریاضی 3 و پایه
-
فصل چهارم: مشتق
| آزمون شماره 193
1- تابع $f(x) = \left\{ {\begin{array}{*{20}{c}}{|{x^2} - x|}&{}&{x < 1}\\{{x^2} + ax + b}&{}&{x \ge 1}\end{array}} \right.$ در $x = 1$ مشتق‌پذیر است. حاصل $a + 2b$ کدام است؟
2-
اگر $\underset{h\to ۰}{\mathop{\lim }}\,\frac{f\left( ۲x+h \right)-f\left( ۲x \right)}{h}=۸{{x}^{۳}}-۲x$ باشد، مشتق تابع $y=f\left( ۳x-۱ \right)$ در $x=-۱$ کدام است؟
3-
اگر خط $y=-۴x+b$بر تابع $f\left( x \right)={{x}^{۴}}-۶$مماس باشد، مقدار $b$ کدام است؟
4-
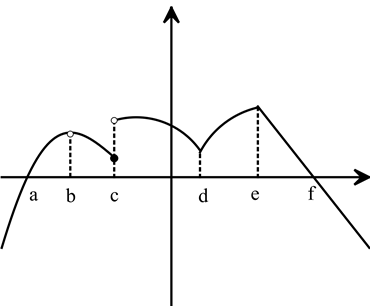
نمودار تابع f به صورت زیر داده شده است. در چند نقطه از دامنه تابع، تابع مشتق پذیر نمی‌باشد؟
5- تابع \[f(x) = \sqrt[3]{{2{x^2} + ax - 21}}\] در نقاط \[x = - 3\] و \[x = b\] مماس قائم دارد. فاصلۀ این دو خط کدام است؟