شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل دوم : هندسه
| آزمون شماره 3586
1- قطر یک ذوزنقه با قاعدة کوچک 4، آن را به دو قسمت تقسیم می‌کند، نسبت مساحت مثلث کوچکتر ایجاد شده به مساحت ذوزنقه ${0_/}4$ است. طول قاعدة بزرگ ذوزنقه کدام است؟
2- حداکثر چند نقطه روی محیط مثلث متساوی‌الاضلاع وجود دارد که از محل برخورد عمود منصف اضلاع آن به یک فاصله باشد؟
3-
در شکل زیر، مثلث $\mathop {ABC}\limits^\Delta $ متساوی‌الساقین است و زوایای ${\hat A_1}$ و ${\hat B_1}$ مکمل یکدیگر هستند. اگر $AC = 2BD$ باشد، حاصل $\frac{{EC}}{{ED}}$ کدام است؟
4-
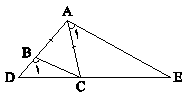
در مثلث ABC در شکل مقابل، پاره‌خط‌های AE و AF را طوری رسم می‌کنیم که ${\hat A_1} = \hat C$ و ${\hat A_2} = \hat B$ باشد. اگر $BE = 8$ و $EF = 14$ و $FC = 18$ باشد، محیط مثلث AEF کدام است؟
5-