شرکت در آزمون آنلاین هندسه 1 - فصل اول: ترسیم های هندسی و استدلال | آزمون شماره 5344

مثلث ABC با زاویه‌های \[\hat A = 45^\circ \] و \[\hat B = 65^\circ \] با مثلث MNP که در آن \[\hat P = 70^\circ \] متشابه است. اگر \[MN = 12\] و \[\frac{{{S_{M\mathop N\limits^\Delta P}}}}{{{S_{A\mathop B\limits^\Delta C}}}} = \frac{3}{4}\] باشد، کدام گزینه صحیح است؟

در مثلث ABC، ${h_a}{\kern 1pt} = 8$ و ${m_a}{\kern 1pt} = 10$ می‌باشد. مقدار ضلع BC کدام‌یک از گزینه‌های زیر باشد تا در مثلث ABC زاویة B منفرجه شود؟

در شکل مقابل \[\hat B = {\hat A_1}\] و \[B\hat AC = 100^\circ \]، زاویه C چند درجه است؟

توی شکل به جای آلفا نوشته شود ۱۰درجهوشکل در پاسخ هم کپی شود.

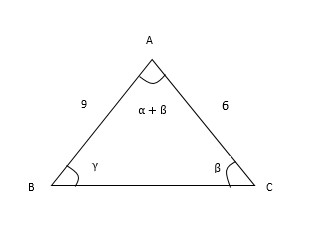
اگر در مثلث ABC اندازه تمامی اضلاع صحیح باشد حداقل اندازه ممکن برای ضلع BC را a  و حداکثر اندازه ممکن برای ضلع BC را b می نامیم ،آنگاه b-a کدام است؟

هر سه زاویه مثلث $ABC$ تند (حاده) هستند. فرض کنید $\hat{B}=۲\hat{C}$ و $AC=۱۰$. ارتفاع $\text{AH}$ را رسم کرده و ضلع $\text{AB}$ را از طرف $\text{B}$ به اندازه $\text{BH}$ امتداد دهید تا به نقطه $\text{E}$ برسید. $\text{E}$ را به $\text{H}$ وصل کنید و امتداد دهید تا ضلع $\text{AC}$ را در $\text{M}$ قطع کند. اندازه پاره خط $MH$ چقدر است؟