شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل ششم : حد و پیوستگی
| آزمون شماره 444
1-
با توجه به نمودار تابع f و g، حاصل $\mathop {\lim }\limits_{x \to 1} fog(x)$ برابر است با:
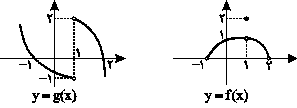
2-
اگر $f(x)=\begin{cases}۲x^۲+۲&x\in\mathbb{Z}\\۱+۲x&x\notin\mathbb{Z}\end{cases}$ باشد، حاصل $\lim_{x\rightarrow\sqrt۲}f(x)-\lim_{x\rightarrow۱}f(x) $ کدام است؟
3-
تعداد نقاط ناپیوستگی تابع $f\left ( x \right )=\left\{\begin{matrix} ۳x-۲ &\left | x \right |> ۱ \\ x^{۲}+x\left [ x \right ] &\left | x \right | \leq ۱ \end{matrix}\right.$ کدام است؟
4-
اگر نمودار تابع f به صورت مقابل باشد، حاصل $۲\lim_{x→۱^- }f(x)-f(۱)+\lim_{x→۱^+}f(x)$ کدام است؟
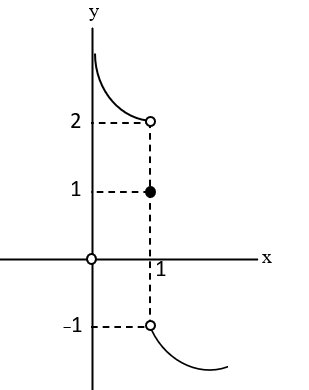
5-
اگر $f\left( x+۱ \right)=\frac{{{x}^{۲}}-x}{۱-\sqrt{x+۱}}$باشد آن گاه $\underset{x\to ۱}{\mathop{\lim }}\,f\left( x \right)$ کدام است؟