 شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 5153
شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 5153
1- ذوزنقه با طول قاعدههای 4 و 9 و ساقهای به طول 5 و 7 مفروضاند. محیط مثلث بزرگتری که از برخورد امتدادهای دو ساق ذوزنقه به دست میآید. کدام است؟
2-
در شکل زیر، چهار نقطة M، N، P و Q طوری روی یک خط قرار گرفتهاند که $\frac{{MN}}{{NP}} = \frac{{MP}}{{PQ}} = \frac{4}{3}$، اگر $MQ = 14$ باشد، طول پارهخط PQ کدام است؟
3-
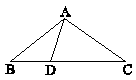
در شکل زیر $AB = AC$، $AD = CD$ و $BD = 4$. اگر نصف طول ضلع AB واسطة هندسی بین اضلاع BD و CD باشد، طول AC کدام است؟
4-
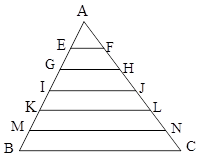
در مثلث ، پارهخطهایی به موازات ضلع BC رسم کردهایم؛ بهطوری که ضلع AB را به شش قسمت مساوی تقسیم کردهاند. اگر $KL = {3_/}2$ باشد، طول پارهخط BC چقدر است؟
5- اگر $\frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = \frac{a}{b}$، حاصل عبارت ${(\frac{{a - c}}{{b - c}})^2}$ با کدام گزینه برابر است؟ (همۀ مخرجها مخالف صفر است.)